No, We Don't Have to Choose Batch Sizes As Powers Of 2
Regarding neural network training, I think we are all guilty of doing this: we choose our batch sizes as powers of 2, that is, 64, 128, 256, 512, 1024, and so forth. (Here, the batch size refers to the number of training examples in each minibatch when we train a neural network with backpropagation via a stochastic gradient descent-based optimization algorithm.)
Allegedly, we do this out of habit and because it’s a standard convention. This is because we were once told that choosing batch sizes as powers of 2 helps improve the training efficiency from a computational perspective.
There are some valid theoretical justifications for this, but how does it pan out in practice? We had some discussions about that in the last couple of days, and here I want to write down some of the take-aways so I can reference them in the future. I hope you’ll find this helpful as well!
The Main Ideas and Theories Behind It
Before we look at hands-on benchmark results, let’s briefly go over the main ideas behind choosing batch sizes as powers of 2. The following two subsections will briefly highlight the two main arguments: memory alignment and floating-point efficiency.
Memory Alignment
One of the main arguments for choosing batch sizes as powers of 2 is that CPU and GPU memory architectures are organized in powers of 2. Or, more precisely, there is the concept of a memory page, which is essentially a contiguous block of memory. If you are using macOS or Linux, you can check the page size by executing getconf PAGESIZE in the terminal, which should return a number that is a power of 2.
The idea is to fit one or multiple batches neatly onto one page to aid parallel processing in GPUs. Or in other words, we choose batch sizes of 2 for better memory alignment. This is analogous (and probably inspired by) choosing power-of-two textures when working with OpenGL and DirectX in video game development and graphics design.
Matrix Multiplication and Tensor Cores
Going into a little more detail, Nvidia has a Matrix Multiplication Background User’s Guide that explains the relationship between matrix dimensions and computational efficiency for graphics processing units (GPUs). So, rather than choosing matrix dimensions as powers of 2, this article recommends choosing matrix dimensions as multiples of 8 for mixed-precision training on GPUs with Tensor Cores. But, of course, there is an overlap between those two:

Why multiples of 8? This has something to do with matrix multiplications. Suppose we have the following matrix multiplication between matrices \(A\) and \(B\):
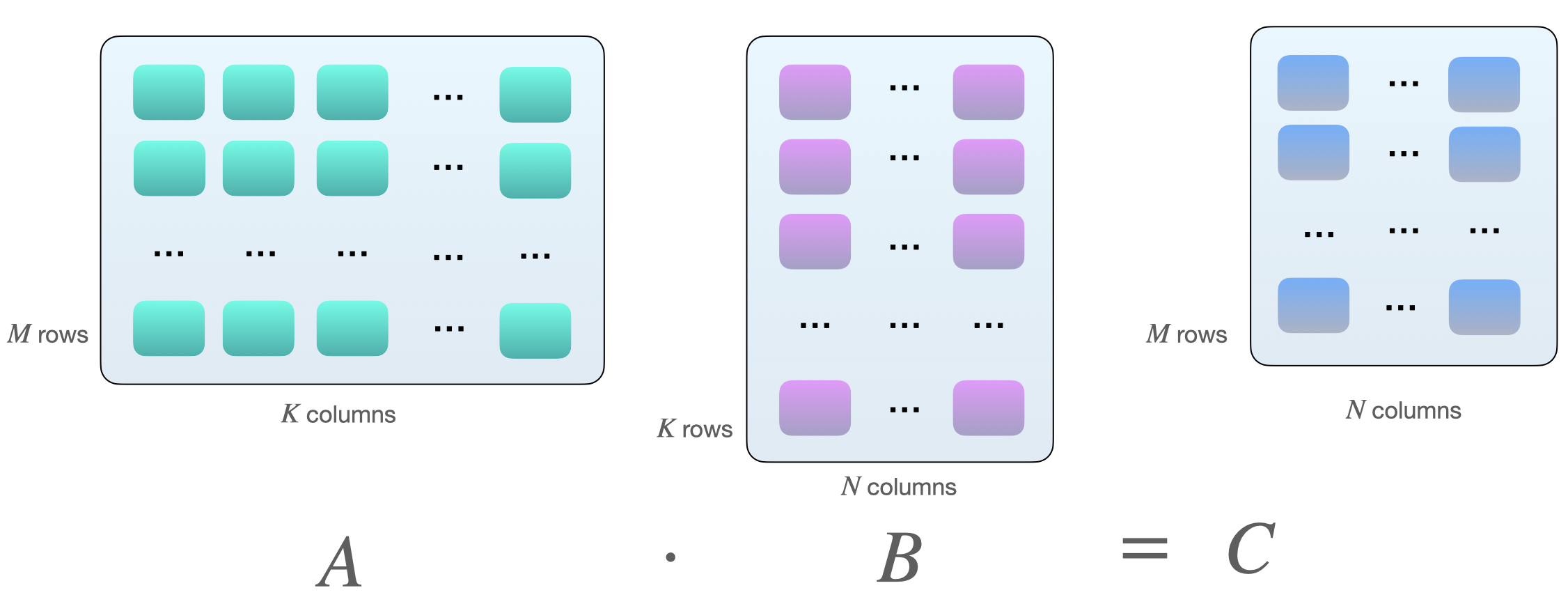
One way to multiply the two matrices \(A\) and \(B\) is by computing dot products between the row vectors of matrix \(A\) and the column vectors of matrix \(B\). As illustrated below, these are dot-products of pairs of \(k\)-element vectors:
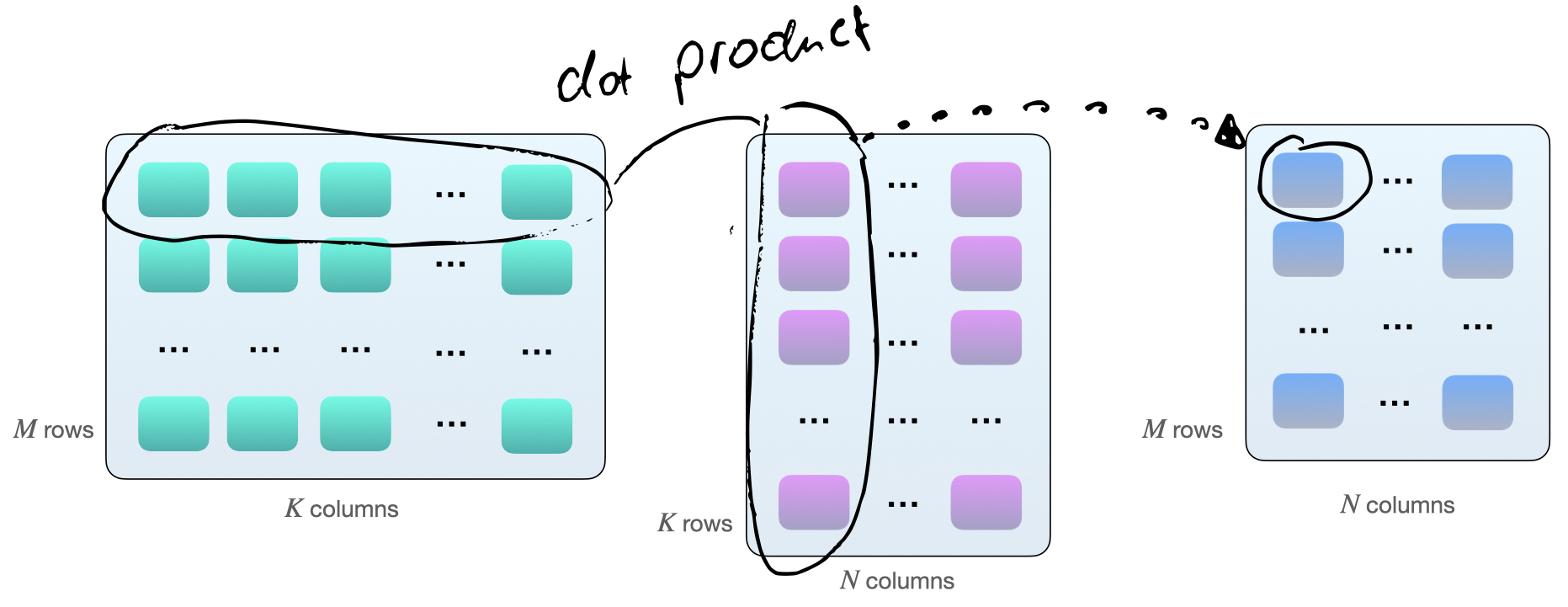
Each dot product consists of one “add” and one multiply” operation, and we have \(M \times N\) of such dot products. So, in total, we have \(2 \times M \times N \times K\) floating point operations (FLOPS).
(Now, that’s not exactly how matrices are multiplied on a GPU; matrix multiplications on the GPU involve tiling.)
Now, if we use GPUs with Tensor Cores, such as V100s, the computational efficiency is better when the matrix dimensions (\(M\), \(N\), and \(K\)) are aligned to multiples of 16 bytes (according to this guide by Nvidia). In the case of FP16 mixed-precision training, multiples of 8 are optimal for efficiency.
Often, the dimensions \(K\) and \(N\) are determined by the neural network architecture (although we have some wiggle-room if we design our own). However, the batch size (here: \(M\)) is usually something we can fully control.
So, assuming that batch sizes as multiples of 8 are theoretically most efficient for GPUs with Tensor Cores and FP16 mixed precision training, let’s investigate how much of a difference we actually notice in practice.
A Simple Benchmark
To see how different batch sizes affect training in practice, I ran a simple benchmark training a MobileNetV3 (large) for 10 epochs on CIFAR-10 – the images are resized to \(224 \times 224\) to reach proper GPU utilization. Here, I ran the training on V100 cards with 16bit native automatic mixed-precision training, which uses the GPUs’ Tensor Cores more efficiently.
If you would like to run it yourself, the code is available in this GitHub repository: https://github.com/rasbt/b3-basic-batchsize-benchmark.
Small Batch Size Benchmarks
I started with a small benchmark around batch size 128. The “Train Time” corresponds to training the MobileNetV3 for 10 epochs on CIFAR-10. Inference time means evaluating the model on the 10k images in the test set.
| Batch Size | Train Time | Inference Time | Epochs | GPU | Mixed Precision |
|---|---|---|---|---|---|
| 100 | 10.50 min | 0.15 min | 10 | V100 | Yes |
| 127 | 9.80 min | 0.15 min | 10 | V100 | Yes |
| 128 | 9.78 min | 0.15 min | 10 | V100 | Yes |
| 129 | 9.92 min | 0.15 min | 10 | V100 | Yes |
| 156 | 9.38 min | 0.16 min | 10 | V100 | Yes |
|
Looking at the table above, let’s consider the batch size 128 as our reference point. It appears that decreasing the batch size by one (127) or increasing the batch size by 1 (129) indeed results in a slightly slower training performance. However, the difference here is barely noticeable, and I would consider it negligible.
Decreasing the batch size by 28 (100) results in a more noticeably slower performance. This is likely because the model now needs to processes more batches than before (50,000 / 100 = 500 vs. 50,000 / 128 = 390). Likely for similar reasons, we can observe a faster training time when we increase the batch size by 28 (156).
Max Batch Size Benchmarks
The batch sizes in the previous section were relatively small given the MobileNetV3 architecture and input image sizes, so the GPU utilization was around 70%. To investigate the training time differences when the GPU is under full load, I increased the batch size to 512 such that the GPU showed near 100% computing utilization:
| Batch Size | Train Time | Inference Time | Epochs | GPU | Mixed Precision |
|---|---|---|---|---|---|
| 511 | 8.74 min | 0.17 min | 10 | V100 | Yes |
| 512 | 8.71 min | 0.17 min | 10 | V100 | Yes |
| 513 | 8.72 min | 0.17 min | 10 | V100 | Yes |
(Batch sizes larger than 515 were not possible due to GPU memory limitations.)
Again, as we saw earlier, a batch size as a power of 2 (or multiple of 8) does make a small but barely noticeable difference.
Multi-GPU Training
The previous benchmarks evaluated the training performance on a single GPU. However, it is more common to train deep neural networks on multiple GPUs nowadays. So, let us have a look at how the numbers compare for multi-GPU training below.
| Batch Size | Train Time | Epochs | GPU | Mixed Precision |
|---|---|---|---|---|
| 255 | 2.95 min | 10 | 4xV100 | Yes |
| 256 | 2.87 min | 10 | 4xV100 | Yes |
| 257 | 2.86 min | 10 | 4xV100 | Yes |
(Note that the inference speeds were omitted because we would typically still use a single GPU for inference in practice. Also, I could not run the benchmark with batch size 512 due to memory constraints on the GPU, so I lowered it to 256.)
As we can see, this time, the power-of-2 and multiple-of-8 batch size (256) is not faster than 257.
Here, I used DistributedDataParallel (DDP) as the default multi-GPU training strategy. However, readers are welcome to repeat the experiments with a different multi-GPU training strategy. The code on GitHub supports --strategy ddp_sharded (fairscale), ddp_spawn, deepspeed, and others.
Benchmarking Caveats: Real-World Vs. Lab
It’s important to highlight that there are a few caveats with all the benchmarks above. For instance, I only ran each setting once. Ideally, we want to repeat these runs multiple times and report the average and standard deviation. (However, this would likely not affect our conclusion that there is no substantial difference in performance.)
Also, while I ran all benchmarks on the same machine (which is a good thing), I ran them in consecutive order without long waiting periods between runs. So, it may mean that the base GPU temperature may have been different between runs and could have affected the timinings slightly.
I ran the benchmarks to mimick a real-world use case, that is, training an off-the-shelf architecture with relatively common settings in PyTorch. However as Piotr Bialecki rightfully pointed out, the training speeds could be slightly improved by setting torch.backends.cudnn.benchmark = True.
Additional Resources and Discussions
As Ross Wightman mentioned, he also does not believe that choosing batch sizes as powers of 2 makes a noticeable difference. However, selecting multiples of 8 might be important for certain matrix dimensions. Furthermore, Ross Wightman points out that the batch size is critical when working with TPUs. (Unfortunately, I don’t have easy access to TPUs and don’t have any benchmark comparisons.)
If you are interested in additional GPU benchmarks, check out Thomas Bierhance’s excellent article here. This is especially interesting if you are looking for comparisons
-
on graphics cards without Tensor Cores;
-
without mixed-precision training;
-
on convolution-free vision transformers like DeiT.
An interesting experiment by Rémi Coulom-Kayufu shows that power-of-2 batch sizes are actually bad. It appears that for convolutional neural networks, a good batch size can be computed via \(\text{batch size}=int((n \times (1<<14)\times SM)/(H\times W\times C))\). Here, \(n\) is an integer and \(SM\) the number of GPU cores (for example, 80 for V100 and 68 for RTX 2080 Ti).
Conclusions
Based on the benchmark results shared in this article, I don’t believe that choosing a batch size as a power of 2 or multiple of 8 makes a noticeable difference in practice.
However, in any given project, let it be a research benchmark or a real-world application of machine learning, there are already so many knobs to tune. So, choosing batch sizes as powers of 2 (that is, 64, 128, 256, 512, 1024, etc.) can help keep things more straightforward and manageable. Also, if you are interested in publishing academic research papers, choosing your batch size as a power of 2 will make your results look less like cherry-picking.
While sticking to batch sizes as powers of 2 can help constrain the hyperparameter search space, it’s important to highlight that batch size is still a hyperparameter. Some argue that smaller batch sizes help with generalization performance, while others recommend increasing the batch size as much as possible.
Personally, I find that the optimal batch size highly depends on the neural network architecture and loss function. For instance, in a recent research project using an identical ResNet architecture, I found that the optimal batch size can range between 16 and 256 depending on the loss function. So, I recommend always considering tuning the batch size as part of your hyperparameter optimization search. However, if you can’t use a batch size of 512 due to memory limitations, you don’t have to drop down to 256. Considering a batch size of 500 first is perfectly fine.

If you read the book and have a few minutes to spare, I'd really appreciate a brief review. It helps us authors a lot!
Your support means a great deal! Thank you!